circuito eléctrico en serie

Un circuito en serie es una configuración de conexión en la que los bornes o terminales de los dispositivos (generadores, resistencias, condensadores, interruptores, entre otros) se conectan secuencialmente. La terminal de salida de un dispositivo se conecta a la terminal de entrada del dispositivo siguiente.

_calculo de resistencia en total: método uno resistencia en serie

la resistencia en serie consiste simplemente en conectar la “salida” de una resistencia a la “entrada” de otra en un circuito. Cada resistencia adicional colocada en un circuito se agrega a la resistencia total de dicho circuito.

• La fórmula para calcular el total de un número “n” de resistores en serie es:
  
  R_eq = R₁ + R₂ + .... R_n
  Es decir, todas los resistores en serie simplemente se suman. Por ejemplo, considera la posibilidad de hallar la resistencia equivalente en la imagen de abajo.
• En este ejemplo,
  R₁ = 100 Ω and R₂ = 300Ω) están conectadas en serie. R_eq = 100 Ω + 300 Ω = 400 Ω

resistencia en paralelo

las resistencias en paralelo ocurren cuando las “entradas” de dos o más resistores están unidas y las “salidas” están unidas.

• La ecuación para calcular el total de resistores “n” en paralelo es:
  
  R_eq = 1/{(1/R₁)+(1/R₂)+(1/R₃)..+(1/R_n)}
• Aquí hay un ejemplo, dadas R₁ = 20 Ω, R₂ = 30 Ω, y R₃ = 30 Ω.
• La resistencia total equivalente para los 3 resistores en paralelo es:
  
  R_eq = 1/{(1/20)+(1/30)+(1/30)}
  
  = 1/{(3/60)+(2/60)+(2/60)}
  
  = 1/(7/60)=60/7 Ω = aproximadamente 8,57 Ω.

circuitos combinados en serie y en paralelo 

circuito eléctrico paralelo su calculo de resistencia total medición de corriente

una red combinada es una combinación de circuitos en serie y en paralelo conectados juntos. Considera la posibilidad de hallar la resistencia equivalente de la red mostrada más abajo.

• Vemos que los resistores R₁ y R₂ están conectados en serie. Entonces su resistencia equivalente (la cual denotaremos por R_s) es:
  
  R_s = R₁ + R₂ = 100 Ω + 300 Ω = 400 Ω.
  
  .
• Luego, vemos que los resistores R₃ y R₄ están conectados en paralelo, por lo que su resistencia equivalente (la cual denotaremos por R_p1) es:
  
  R_p1 = 1/{(1/20)+(1/20)} = 1/(2/20)= 20/2 = 10 Ω
• Luego vemos que los resistores R₅ and R₆ también están conectados en paralelo, por lo que su resistencia equivalente (la cual denotaremos por R_p2) es:
  
  R_p2 = 1/{(1/40)+(1/10)} = 1/(5/40) = 40/5 = 8 Ω
• Ahora tenemos un circuito con los resistores R_s, R_p1, R_p2 and R₇ conectados en serie. Estos resistores simplemente se suman para obtener la resistencia equivalente R₇ de la red que se nos dio originalmente.
  
  R_eq = 400 Ω + 20Ω + 8 Ω = 428 Ω.

3.1.3. RESISTENCIA ELÉCTRICA

Se denomina resistencia eléctrica, R, de una sustancia, a la oposición que encuentra la corriente eléctrica para recorrerla. Su valor se mide en ohmios y se designa con la letra griega omega mayúscula (Ω). La materia presenta 4 estados en relación al flujo de electrones. Éstos son Conductores, Semi-conductores, Resistores y Dielectricos. Todos ellos se definen por le grado de oposición a la corriente electrica (Flujo de Electrones).

Esta definición es válida para la corriente continua y para la corriente alterna cuando se trate de elementos resistivos puros, esto es, sin componente inductiva ni capacitiva. De existir estos componentes reactivos, la oposición presentada a la circulación de corriente recibe el nombre de impedancia.

Según sea la magnitud de esta oposición, las sustancias se clasifican en conductoras, aislantes y semiconductoras. Existen además ciertos materiales en los que, en determinadas condiciones de temperatura, aparece un fenómeno denominado superconductividad, en el que el valor de la resistencia es prácticamente nula.

La resistencia electrica se mide con el Ohmímetro es un aparato diseñado para medir la resistencia eléctrica en ohmios. Debido a que la resistencia es la diferencia de potencial que existe en un conductor dividida por la intensidad de la corriente que pasa por el mismo, un ohmímetro tiene que medir dos parámetros, y para ello debe tener su propio generador para producir la corriente eléctrica.

Imagen de un grupo de resistores

3.1.4. LA LEY DE OHM

Como la resistencia eléctrica en un circuito es muy importante para determinar la intensidad del flujo de electrones, es claro que también es muy importante para los aspectos cuantitativos de la electricidad. Se había descubierto hace tiempo que, a igualdad de otras circunstancias, un incremento en la resistencia de un circuito se acompaña por una disminución de la corriente. Un enunciado preciso de esta relación tuvo que aguardar a que se desarrollaran instrumentos de medida razonablemente seguros. En 1820, Georg Simon Ohm, un maestro de escuela alemán, encontró que la corriente en un circuito era directamente proporcional a la diferencia de potencial que produce la corriente, e inversamente proporcional a la resistencia que limita la corriente. Expresado matemáticamente:

donde I es la corriente, V la diferencia de potencial y R la resistencia.

Esta relación básica lleva el nombre del físico que más intervino en su formulación: se llama Ley de Ohm.

Si se reemplaza el signo de proporcionalidad de la Ley de ohm por un signo de igual, se tiene:

 

Ley de Ohm para determinar corriente eléctrica (Amperios)

Despejando le ecuación anterior, se encuentran dos ecuaciones más:

Ley de Ohm para determinar valores de resistencias (Ohmios)

Ley de Ohm para determinar voltaje (Voltios)

De esta forma, la Ley de Ohm define la unidad de resistencia eléctrica así como también el voltaje y la corriente, haciendo sencillos despejes de las ecuaciones presentadas, siempre y cuando se tengan dos valores conocidos y una sóla incógnita.

3.2. TIPOS DE CONEXIÓN

3.2.1. CONEXIÓN SERIE

Dos o más resistencias se encuentran conectadas en serie cuando al aplicar al conjunto una diferencia de potencial, todas ellas son recorridas por la misma corriente. El esquema de conexión de resistencias en serie se muestra así:

Resistencias conectadas en serie

3.2.2. CONEXIÓN PARALELO

Dos o más resistencias se encuentran en paralelo cuando tienen dos terminales comunes de modo que al aplicar al conjunto una diferencia de potencial, UAB, todas la resistencias tienen la misma caída de tensión, UAB. Una conexión en paralelo se muestra de la siguiente manera:

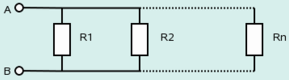
Resistencias conectadas en paralelo

3.2.3. CONEXIÓN SERIE PARALELO

En una conexión serie paralelo se pueden encontrar conjuntos de resistencias en serie con conjuntos de resistencias en paralelo, como se muestra a continuación:

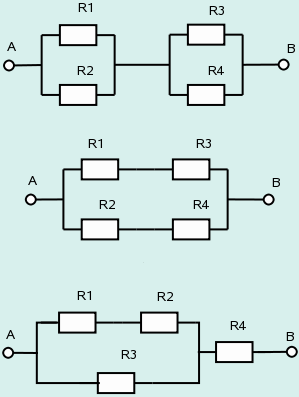
Resistencias conectadas en serie paralelo

3.3. RESISTENCIAS EN SERIE Y DIVISOR DE VOLTAJE

El divisor de voltaje es una herramienta fundamental utilizada cuando se desean conocer voltajes de resistencias específicas, cuando se conoce el voltaje total que hay en dos resistencias. Es necesario considerar que el divisor de voltaje funciona para analizar dos resistencias, y que si se quieren determinar voltajes de más de dos resistencias utilizando el divisor de voltaje, deberá hacerse sumando resistencias aplicando paso a paso el divisor de voltaje de dos en dos, hasta llegar al número total de resistencias. Esto es muy útil porque en muchas ocasiones no es posible aplicar la Ley de Ohm debido a que sólo se tiene el valor de las resistencias, pero no se conoce el voltaje. Es entonces que se aplica el divisor de voltaje, con las siguientes fórmulas y de acuerdo al esquema mostrado a continuación:

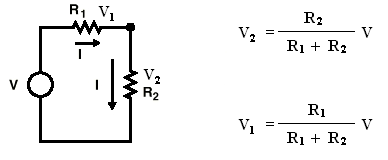
Otra herramienta importante es el divisor de corriente, que funciona para resistencias en paralelo. Sin embargo no fue necesario utilizarla en esta práctica, pues fue en las conexiones en paralelo ya se tenían los voltajes (que eran el mismo de la fuente por tratarse de conexión en paralelo) y los valores de las resistencias, por lo que las corrientes se encontraron fácilmente a través de la Ley de Ohm.

4. DESARROLLO Y SOLUCIÓN DE LA GUÍA DE TRABAJO UTILIZADA EN LA PRÁCTICA

4.1. MATERIAL Y EQUIPO

• Resistencia de diferentes valores
• Breadboard
• Alambre #24
• Tester análogos o digitales
• Fuente de voltaje

4.2. CIRCUITO SERIE

Cuando un grupo de resistencias se conecta como en la figura 1, por todas ellas fluye la misma corriente y se dice que las resistencias están conectadas en serie.

Figura 1

4.2.1. PROCEDIMIENTO

1. Alambrar el circuito de la figura.
2. Pedir revisión.
3. Tomar lecturas de voltaje y resistencia, anotándolas en la tabla de la figura 1.

Datos	R1	R2	R3	Re	V1	V2	V3	E	I1	I2	I3	I
Teóricos	5600	1500	470	7570	6.66	1.78	0.56	9	0.00119	0.00119	0.00119	0.00119
Experi- mentales	5600	1500	470	7570	6.5	1.9	0.6	9	0.0012	0.0012	0.0012	.0012

Tabla de la Figura 1

NOTA: Las medidas de la tabla están en Ohmios (Ω) para las resistencias, Voltios (V) para los voltajes y Amperios (A) para las corrientes.

4.2.2. PREGUNTAS

1. R// Este proceso fue justamente el que se realizó para plasmar los datos teóricos presentados en la tabla de la Figura 1. Para ello se contaba únicamente con el valor de la fuente, que fue de 9V, y con los valores de las resistencias, que se encontraron utilizando el código de colores para determinar los valores correspondientes en ohmios para cada resistencia.
   Primeramente se redujo determinó la resistencia equivalente, sumando las tres resistencias en serie y llegando a tener una sola. Luego de eso, el voltaje en la resistencia equivalente era de 9V, es decir el mismo de la fuente por tratarse de una conexión en paralelo. A continuación se utilizó el divisor de voltaje y se fue retrocediendo en los diagramas hechos cuando se habían venido uniendo resistencias, y fue así como finalmente, teniendo el voltaje en cada resistencia así como el valor en ohmios de estas mismas, se utilizó la Ley de Ohm para determinar la corriente de cada resistencia, con la ecuación I = V / R. Fue de esa manera como se encontraron los voltajes y corrientes para cada resistencia de la conexión en serie.
2. Calcular teóricamente el voltaje y la corriente en cada elemento del circuito.
   R// Los valores de la corriente son los mismos para cualquier resistencia por la razón que se está trabajando con un circuito conectado en serie, donde siempre se cumple que la corriente es la misma para cada uno de los elementos del circuito.
3. ¿Cómo son entre sí los valores de la corriente en los diferentes elementos de un circuito serie?
   R// Sí porque si la posición relativa de las resistencias fuera una conexión en paralelo, el valor de la corriente no sería el mismo para cada resistencia, pero debido a que la posición relativa de cada resistencia se encuentra con una conexión en serie, los valores de la corriente son los mismos para cada resistencia, por lo cual se concluye que la posición relativa de las resistencias SÍ interviene en el valor de la corriente.
4. ¿Interviene en el valor de la corriente, la posición relativa de las resistencias?
   R// La fuerza electromotriz aplicada o el voltaje aplicado por la fuente fue de 9V, y es precisamente la suma de las caídas de potencial en las tres resistencias, es decir que al sumar los voltajes que hay en las resistencias 1, 2 y 3, se obtiene el valor de 9V, de esta manera: (6.66 + 1.78 + 0.56)V = 9V.
5. Compare la fuerza electromotriz aplicada con la suma de las caídas de potencial en las tres resistencias R1, R2, R3.
   R// La resistencia 1, que era la que tenía mayor número de ohmios (5600Ω), fue precisamente la que produjo mayor voltaje o mayor caída de potencial, ya que se registran 6.66V en esa resistencia, lo cual equivale al 74% del voltaje total (9V) que fue suministrado para el circuito.
6. ¿Cuál resistencia produjo mayor caída de potencial?
   R// Experimentalmente, esto lo calculamos con el tester, colocando sus terminales positiva y negativa correctamente sobre los alambres laterales de la resistencia. De forma teórica, esto se logra utilizando el divisor de voltaje, sabiendo que esta conexión era en serie. El divisor de voltaje es explicado en el marco teórico de este documento.
7. ¿Cómo se calcula la caída de potencial en una resistencia de forma teórica y experimental?
   R// Para esta comprobación, se muestran los cálculos de los valores obtenidos en la práctica, con lo que se tiene lo siguiente:
   I = E / R1 + R2 + R3 è (0.00119A) = (9V) / (5600 Ω) + (1500 Ω) + (470 Ω)
   I = E / Re è (0.00119A) = (9V) / (7570 Ω)
   Con lo anterior se puede observar que en una conexión en serie, una resistencia equivalente es la suma aritmética de cada una de las resistencias. Igualmente se puede ver la utilidad de la Ley de Ohm.
8. Compruebe que en el circuito de la figura 1 se cumple: I = E / R1 + R2 + R3 = E / Re.
   R// Esto se hizo utilizando la breadboard, alambres para hacer las conexiones, la fuente de voltaje y el tester. Los valores obtenidos son los que se muestran en la Tabla de la Figura 1.
9. Calcular de forma experimental el voltaje y la corriente en cada elemento del circuito.
10. Los valores de corriente y voltaje calculados en el paso anterior, ¿coinciden con los correspondientes valores teóricos calculados?

R/ Sí coinciden, pues experimentalmente se realizaron las conexiones en serie para las resistencias tal como se indica en el diagrama de la Figura 1 de esta práctica, y con el tester se midieron voltajes y corrientes en cada una de las tres resistencias del circuito, y son valores muy cercanos a los obtenidos haciendo los cálculos teóricos.

4.3. CIRCUITO PARALELO

Se dice que dos o más resistencias están en paralelo cuando sus terminales están conectadas entre sí formando nodos eléctricos como se muestra en la figura 2.

Figura 2

En el circuito anterior la corriente I, suministrada por la fuente llega al nodo 1 y se reparten en tantos caminos como resistencias en paralelo existan. Si llamamos a estas corrientes I1, I2, I3; las caídas de voltaje en R1, R 2, R 3 son respectivamente:

V1 = I1R1; V2 = I2 R2; V3 = I3 R3

  V = I Re = I1R1 = I2R2 = I3R3

Se deduce que:

I = I1 + I2 + I3, ya que I se divide en el nodo 1 en las tres corrientes de rama I1, I2 e I3.

Luego:

I1 = IRe / R1, I2 = IRe / R2, I3 = IRe / R3

Por tanto:

I = I1 + I2 + I3 = IRe / R1 + IRe / R2 + IRe / R3

I = IRe (1 / R1 + 1 / R2 + 1 / R3)

I (1 / Re) = I (1 / R1 + 1 / R2 + 1 / R3)

2.3.1. PROCEDIMIENTO

1. Alambrar el circuito de la figura 3.
2. Pedir revisión.
3. Tomar lecturas de voltaje y resistencia, anotándolas en la tabla de la figura 2 y 3.

Figura 3

Datos	R1	R2	R3	Re	V1	V2	V3	E	I1	I2	I3	I
Teóricos	5600	1500	470	336.37	9	9	9	9	0.00161	0.006	0.0191	0.0268
Experimentales	5600	1500	470	336.37	9	9	9	9	0.0015	0.006	.018	0.0255

Tabla de las Figuras 2 y 3

NOTA: Las medidas de la tabla están en Ohmios (Ω) para las resistencias, Voltios (V) para los voltajes y Amperios (A) para las corrientes.

4.3.2. PREGUNTAS

1. R// Se contaba inicialmente sólo con el valor del voltaje de la fuente y el valor de cada resistencia, que fue obtenido a través del código de colores para resistencias. Sabiendo que la conexión era en paralelo, el voltaje para cada resistencia por tanto fue el mismo que el de la fuente: 9V. Finalmente se utilizó la Ley de Ohm para encontrar la corriente en cada resistencia, y así se completaron los datos teóricos para la Tabla de las Figuras 2 y 3.
2. Calcular teóricamente el voltaje y la corriente en cada elemento del circuito.
   I = I1 + I2 + I3
   E = V1 + V2 + V3
   R// Para realizar esta comprobación, se sustituyen en las ecuaciones que se quieren comprobar, los valores obtenidos en la práctica:
   I = I1 + I2 + I3 è (0.0268A) = (0.00161A) + (0.006A) + (0.0191A)
   I = E / Re è (0.0268A) = (9V) / (336.37)
   Con lo anterior se observa que en una conexión en paralelo, la corriente total es la suma aritmética de las corrientes en cada una de las resistencias. También se observa la veracidad y utilidad de la Ley de Ohm.
3. Con los datos obtenidos en el paso anterior, compruebe las siguientes ecuaciones:
   R// Este proceso se realizó utilizando la breadboard, alambres para hacer las conexiones, la fuente de voltaje y el tester. Los valores obtenidos son los que se muestran en la Tabla de las Figuras 2 y 3.
4. Calcular de forma experimental el voltaje y la corriente en cada elemento del circuito.
5. Los valores de corriente y voltaje calculados en el paso anterior, ¿coinciden con los correspondientes valores teóricos calculados?

R// Sí coinciden, debido a que experimentalmente se realizaron las conexiones en paralelo para las resistencias tal como se indica en el diagrama de las Figuras 2 y 3 de esta práctica, y con el tester se midieron voltajes y corrientes en cada una de las tres resistencias del circuito, y son valores muy cercanos a los obtenidos haciendo los cálculos teóricos.

4.4. CIRCUITO SERIE PARALELO

4.4.1. PROCEDIMIENTO

1. Alambrar el circuito de la figura 4.
2. Pedir revisión.
3. Tomar lecturas de voltaje y resistencia, anotándolas en la tabla de la figura 4.
4. Calcular el voltaje y la corriente en cada elemento del circuito.

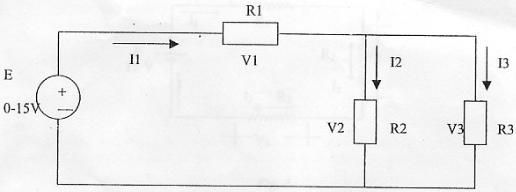
Figura 4

Datos	R1	R2	R3	Re	V1	V2	V3	E	I1	I2	I3	I
Teóricos	5600	1500	470	5957.87	8.46	0.41	0.13	9	0.00151	0.000273	0.000277	0.00151
Experimentales	5600	1500	470	5957.87	8.4	0.45	0.15	9	0.0015	0.0003	0.00026	0.00206

Tabla de la Figura 4

NOTA: Las medidas de la tabla están en Ohmios (Ω) para las resistencias, Voltios (V) para los voltajes y Amperios (A) para las corrientes.

CONCLUSIÓN

Esta práctica ha sido muy provechosa por varias razones, las cuales se resumen en esta conclusión. En primer lugar, se ha practicado el uso del voltímetro y de la breadboard, que es algo muy importante y que seguirá siendo provechoso en nuevas prácticas que se realicen en el futuro.

Los conocimientos de la Ley de Ohm fueron llevados a la práctica y se ha observado cómo la Ley se cumple perfectamente siempre que las conexiones y mediciones son hechas correctamente.

También se aprendió a hacer mediciones de voltajes, resistencias y corrientes eléctricas y a establecer relaciones entre estos valores en base al tipo de conexión con la que se esté trabajando, que puede ser en serie, paralelo y serie paralelo.

Un aprendizaje muy valioso que se obtuvo de esta práctica es también el armar circuitos en los tres tipos de conexión ya mencionados. De la misma forma se aplicaron las propiedades que fueron comprobadas, como por ejemplo que la corriente es la misma en cualquier elemento conectado en serie, o que el voltaje es el mismo en cualquier elemento conectado en paralelo.

Se ha cumplido con los objetivos propuestos para esta práctica, y se desea que este reporte sea de provecho para aquellos que próximamente realicen este tipo de experimentos prácticos de electricidad.

simulador cocodrilo

Crocodile Clips v3.5 es un simulador de circuitos eléctricos en donde podemos poner en práctica lo que sabemos y lo que queremos saber acerca de ellos.